Viši harmonici

10.08.2020.

Viši harmonici u elektro-energetici

Ovaj članak je namenjen inženjerima i cilj nam je da pojasnimo pojam viših harmonika, način merenja, uzroke, snagu potrošača u takvim uslovima i na kraju načine za ograničenje njihovog uticaja. Cilj nam je da budemo praktični i objasnimo suštinu, te ovom prilikom nećemo ulaziti u akademske detalje i složeni matematički aparat.

Osnovni harmonik

Termin „harmonici“ se u teoriji signala koristi da se objasni distorzija (izobličenje) osnovnog signala. U elektroenergetici kao osnovni signal koristi se sinusoida učestanosti 50Hz, tj. trajanje osnovne periode signala je 20 ms. Ova sinusoida se neprestano ponavlja, tj. periodična je. Ovakav čist signal nazivamo osnovna harmonična komponenta, osnovni harmonik ili čak idealna sinusoida. To je signal koji se elektroprivreda trudi da proizvede i prenese do krajnjih potrošača. Naravno, to u praksi nije moguće i mrežni napon uvek ima manje ili veće varijacije amplitude, faznog stava, učestanosti, kao i odstupanje od oblika idealne sinusoide. I tu počinje priča o višim harmonicima.

Primer linearnog uređaja: trenutne vrednosti napona i struje su proporcionalni tokom čitave periode napona.

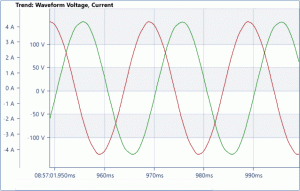
linearni potrošač — Primer linearnog potrošača: trenutne vrednosti napona i struje su proporcionalni tokom čitave periode.

U praksi problem viših harmonika nije bio izražen dok je najveći broj potrošača imao linearnu karakteristiku potrošnje, tj. dok su i napon i struja imali sinusoidalan talasni oblik u kontinuitetu. To je bilo vreme transformatora, sijalica sa užarenom niti, trofaznih asinhronih motora i kondenzatora.

Izvori viših harmonika

Sa razvojem tehnologije u mreži su se pojavili nelinearni potrošači. To su uređaji kod kojih odnos između trenutnih vrednosti napona i struje nije konstantan tokom čitave periode signala, već se menja. To su najčešće uređaji koji koriste energetske pretvarače ili ispravljače za svoje napajanje, a njih je danas veoma mnogo. U industriji to su: jednosmerni motori, pretvarači, frekventni regulatori, indukcione peći, servo motori, fluo cevi, serveri, bazne stanice, solarne elektrane, vetrogeneratori itd… u domaćinstvima to su skoro svi elektronski uređaji: punjači, napajanja za računare, televizore, itd… Uopšte trend u energetici je da se povećava udeo nelinearnih potrošača, jer su veoma komforni i jednostavni za upotrebu. Cena koju plaćamo je prisustvo viših harmonika.

Posledice prisustva viših harmonika nisu samo u izgledu ukupnog signala, već su mnogo ozbiljnije i to je tema posebnog članka.

Nelinearni potrošači

Više harmonike generišu nelinearni uređaji u vašem pogonu: frekventni regulatori, pretvarači, indukcione i elektrolučne peći, fluo svetiljke, jednosmerni motori, solarni invertori, vetro generatori… Zajedničko za sve nelinearne uređaje uređaje jeste da odnos između trenutnih vrednosti napona i struje nije konstantan, već se menja tokom trajanja osnovne periode.

Primer nelinearnog uređaja: odnos struje i napona nije konstantan tokom periode

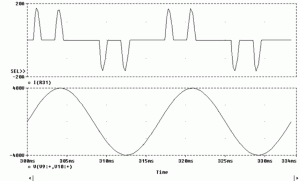
nelinearni potrošač — Primer nelinearnog potrošača: struja nije proporcionalna naponu tokom čitavog trajanja periode.

Ovakvi talasni oblici struje sami po sebi nisu ništa loše, jednostavno način funkcionsanja uređaja je takav da je njegova struja nelinearna, složena. Sa jedne strane takvi uređaji pružaju nam široke mogućnosti koje linearni uređaji ne mogu (kao što je kontrola broja obrtaja, kontrola snage i momenta). Sa druge strane posledica je nastanak viših harmonika i pogoršanje kvaliteta napona.

Furijeova transformacija

Matematički aparat koji koristimo u teoriji kola razvijen je u vreme linearnih potrošača, tj. baziran je na operacijama nad jednostavnim, prostoperiodičnim i neprekidnim signalima. Nelinearni potrošač nam pravi problem kod ovakve analize. Njegovu struju ne možemo predstaviti linearnom, neprekidnom, prostoperiodičnom funkcijom. Onda ne možemo ni koristiti postojeće i jednostavne matematičke metode za analizu. Stoga na scenu stupa čuvena Furijeova transformacija. Ona nam omogućava da jedan složeni, nelinearni talasni oblik precizno razložimo na sumu jednostavnih, prostoperiodičnih funkcija – najčešće sinusnih i kosinusnih funkcija koje nazivamo harmoničnim komponenentama. Jedna komponenta ima osnovnu učestanost, a ostale imaju više učestanosti, po pravilu umnoške osnovne učestanosti. Znači ako je napon u mreži učestanosti 50 Hz, onda neki složeni talasni oblik u elektroenergetici možemo predstaviti kao sumu: osnovne harmončne komponente učestanosti 50Hz (idealna sinusoida) i viših harmoničnih komponenti (opet sinusoide) koje imaju učestanost 100, 150, 200, 250, 300, 350 Hz i tako dalje.

Dekonstrukcija složenog talasnog oblika

I tako, od jednog složenog talasnog oblika, teškog za dalju analizu, dobili smo veći broj jednostavnih signala različite učestanosti, koji se mogu dalje analizirati koristeći postojeći matematički aparat tj. teoriju kola. Furijeova analiza je samo alat koji koristimo da objasnimo ono što se dešava u mreži i u potrošačima, a da nastavimo da koristimo postojeće alate i znanje. Znači procedura kojom složeni talasni oblik predstavljamo kao sumu jednostavnih prostoperiodičnih komponenti različitih učestanosti je samo način da bolje analiziramo taj složeni signal. Bilo koja viša harmonična komponenta, sama po sebi ne postoji izolovano i samostalno, već je deo ukupnog signala.

Da zaključimo, viši harmonici su matematička reprezentacija ili tačnije rečeno matematička dekonstrukcija jednog složenog talasnog oblika. Što je izobličenje veće, to je i sadržaj viših harmonika veći. Postoji čitava oblast matematike koja se time bavi, zove se teorija signala i obuhvata široku oblast signala koji se javljaju u elektrotehnici od mrežnog napona i struje, preko akustičnih pa do radio talasa i dalje. Zadržimo se na elektro-energetici.

Primer dekompozicije signala

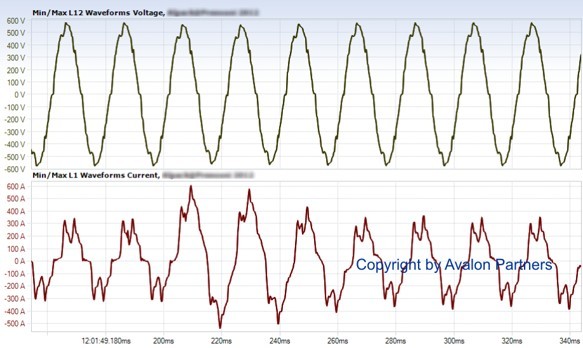
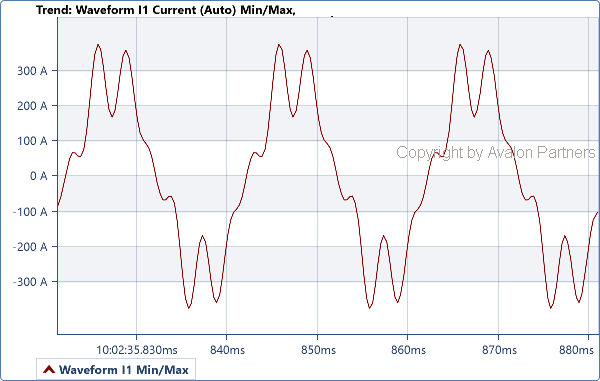
Na slici dole je prikazan slučaj karakterističan za elektroenergetski sistem: nelinearna struja jednog 6-to pulsnog frekventnog regulatora predstavljena je žutom bojom.

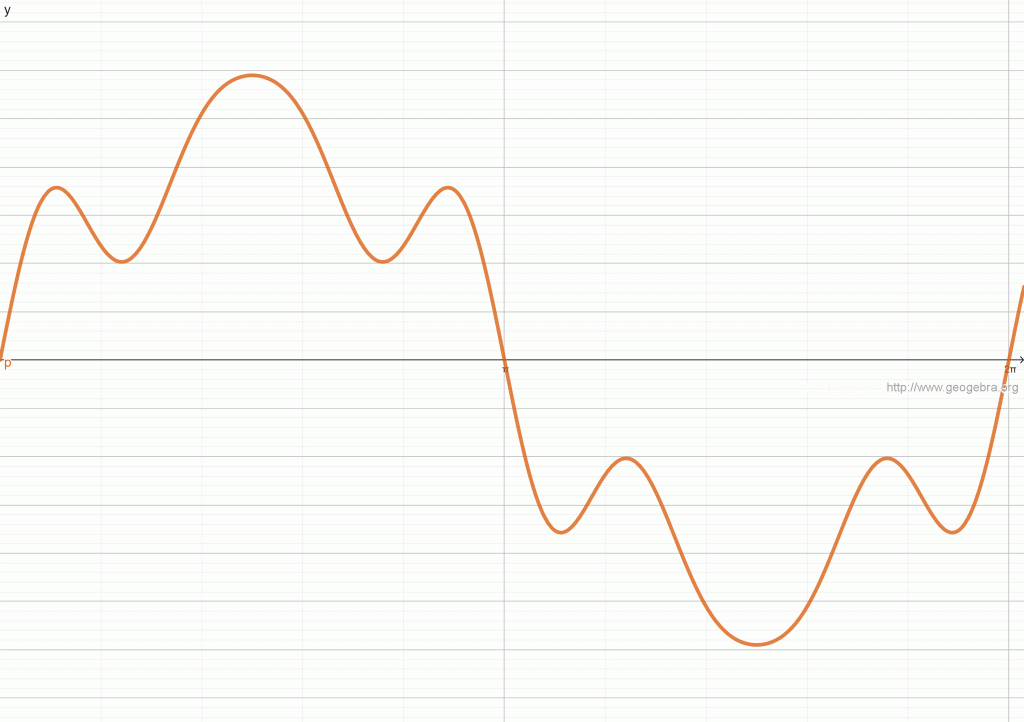
Kada se izvrši dekompozicija tog talasnog oblika na harmonične komponente dobijaju se:

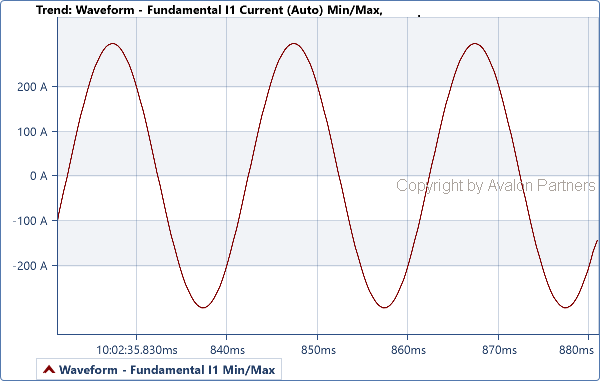
prvi (osnovni) harmonik – nacrtan zelenom bojom, je osnovni sinusoidalni talas koji osciluje sa učestanošću od 50 Hz (osnovna učestanost) što znači da tokom vremenskog intervala od 1 sekunde ovaj talas napravi 50 punih oscilacija;
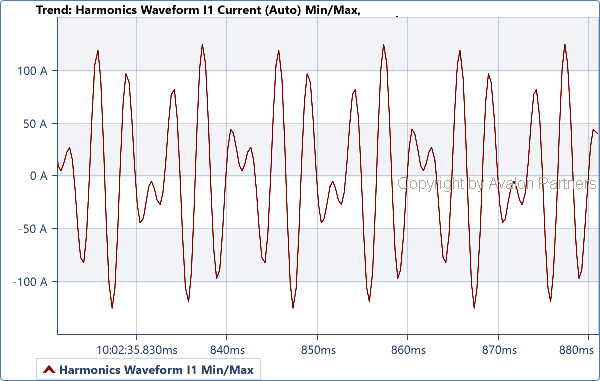
peti harmonik – nacrtan plavom bojom, čija je učestanost 150 Hz, što se vidi u broju perioda (3) koje napravi za jednu periodu osnovnog harmonika.
sedmi harmonik– nacrtan crvenom bojom, čija je učestanost 150 Hz, što se vidi u broju perioda (3) koje napravi za jednu periodu osnovnog harmonika.

Ukupna nelinearna struja sa gornje slike jednaka je sumi osnovnog i svih viših harmonika struje sa donje slike. Svi signali na donjoj slici su linearni, srazmerni sa naponom tokom čitave periode signala, za razliku od ukupne struje.

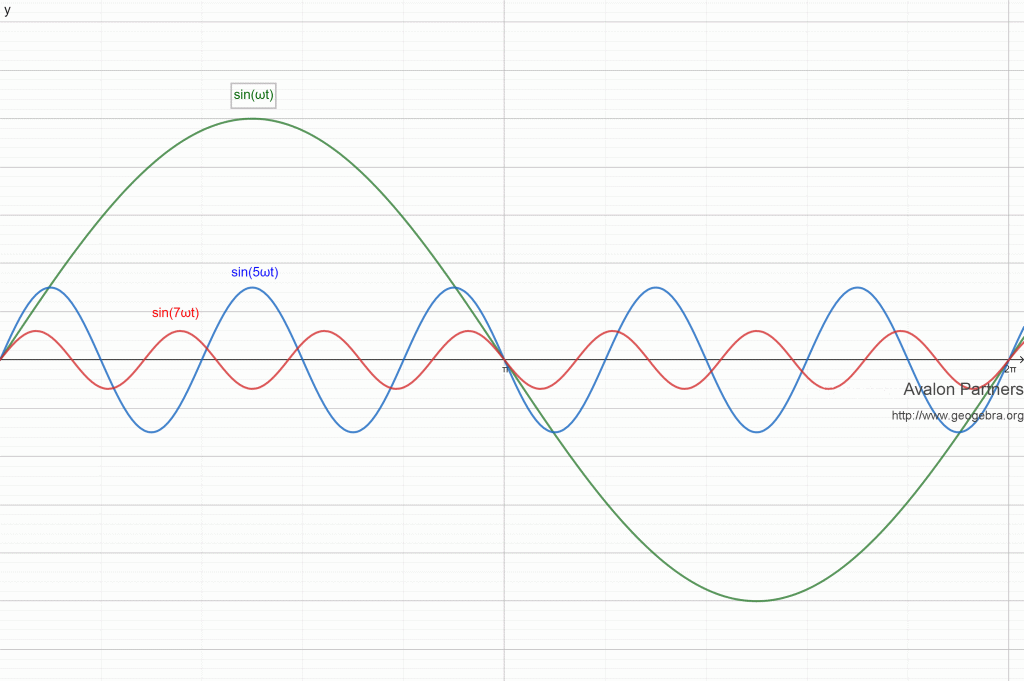
Primer sinteze signala

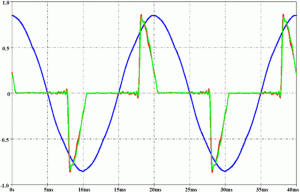
Važno je razumeti da viši harmonici postoje istovremeno sa osnovnim harmonikom, tj. viši harmonici se superponiraju na osnovni harmonik čime dovode do izobličenja osnovnog signala. U sledećem primeru (v. sliku ispod) prikazujemo kako se viši harmonici redom superponiraju na osnovni i povećavaju izobličenje sve dok ne dobijemo ukupni signal – talasni oblik struje frekventnog regulatora 6-to pulsnog tipa. U primerima dole vidi se kako dodavanjem harmoničnih komponenti osnovni signal postaje sve više izobličen. Naglašavam da konačni izgled talasa ne zavisi samo od broja i amplitude viših harmonika već i od njihovog faznog pomeraja u odnosu na osnovni (na slikama su ova dva talasa u fazi), ali nećemo ići tako daleko u ovom članku.

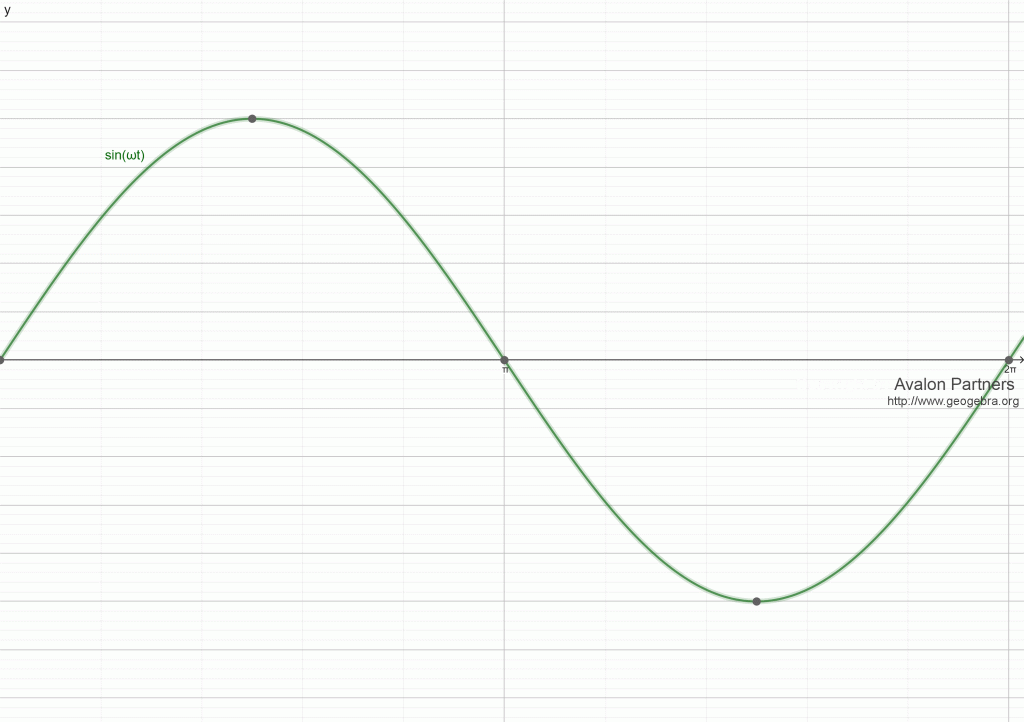
Osnovni harmonik: talasni oblik osnovne učestanosti 50 Hz

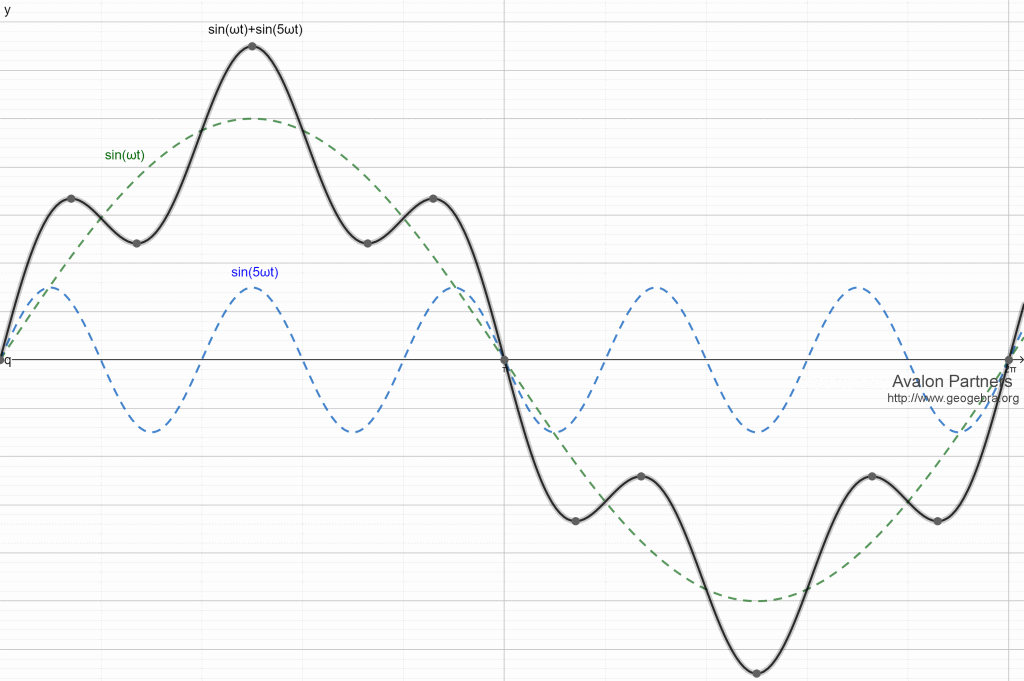
viši harmonici

Superponiranje osnovnog harmonika (50 Hz) i petog harmonika (250 Hz)

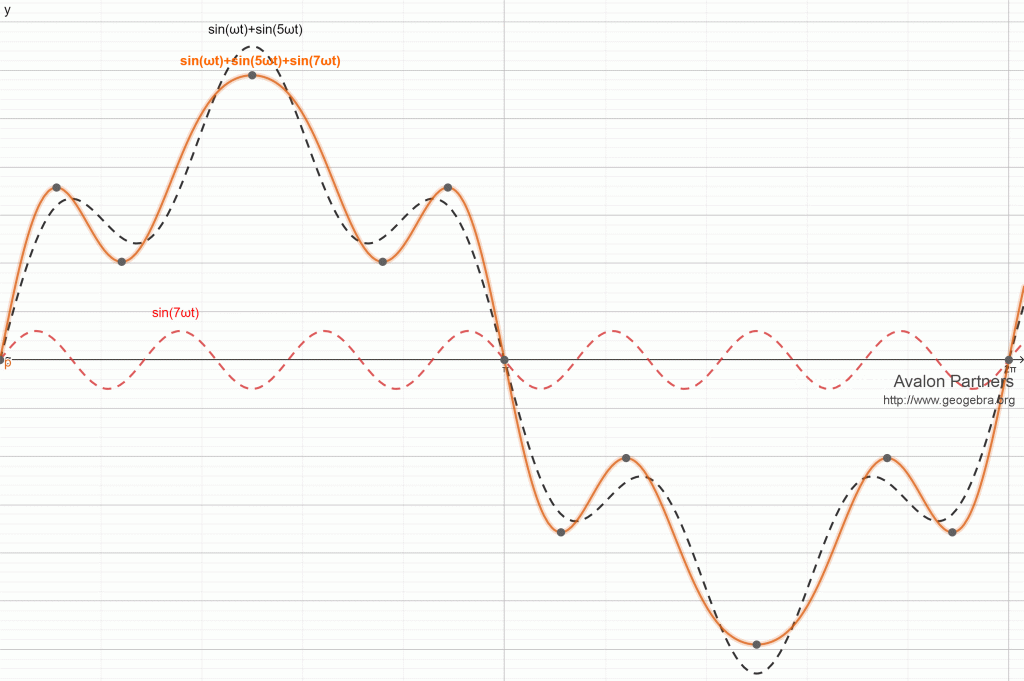
viši harmonici

Superponiranje harmonika: osnovnog, petog i sedmog

Na ovom linku nalazi se interaktivna verzija alata za generisanje signala složenog iz osnovne i viših harmoničnih komponenti.

Kako nastaju viši harmonici

Kao posledica rada nelinearnih potrošača, javlja se složeni oblik struje potrošača koji nije linearno zavistan od napona. Da bi smo mogli analizirati taj složeni oblik istim matematičkim apartom kojim analiziramo i linearne potrošače, vršimo matematičku dekompoziciju signala u sumu jednostavnih prostoperiodičnih signala različitih učestanosti. I to je taj proces (Furijeova transformacija) u kome viši harmonici odjednom postanu vidljivi i definisani. Svaku od tih komponenti možemo analizirati odvojeno ili zajedno sa ostalima. Jednostavno, zar ne? 🙂 Tada kažemo da struja određenog potrošača ima izražen neki harmonik. Na primer 5. i 7. harmonik kod frekventnih regulatora, ili čak 2. ili pak 25. harmonik kod elektrolučnih peći. To što za neki signal kažemo da sadrži više harmonike, samo znači da je taj signal složen. Viši harmonik ne nastaje sam za sebe i nevezano sa ostatkom signala.

Uređaji koji su nelinarni i izvori viših harmonika su: frekventni regulatori, indukcione peći, elektrolučne peći, zavarivačke mašine, elektronski uređaji, računari, fluo rasveta i mnogi drugi.

Evo nekoliko primera:

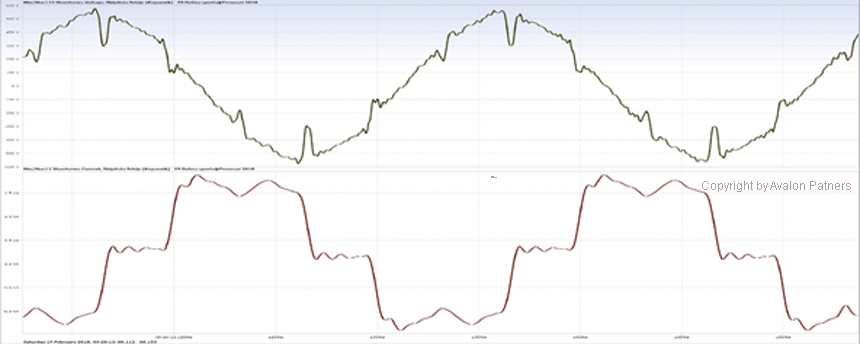
viši harmonici fluo cev — Talasni oblik fluo cev

Svaki od navedenih primera ima svoju oblast primene: regulacija brzine motora, topljenje materijala u peći, regulacija nivoa osvetljenja,… Gore navedene talasne oblike potrebno je dekomponovati u osnovnu i više harmonične komponente i tek onda se mogu analizirati.

Efektivna vrednost struje i viši harmonici

Struja bogata višim harmonicima daleko više opterećuje provodnik i transformator od struje koja sadrži samo osnovni harmonik. Evo pojašnjenja.

Ako su i efektivne vrednosti i-tog višeg harmonika, onda su efektivne vrednosti (ukupna vrednost signala) napona i struje:

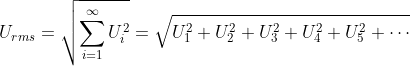
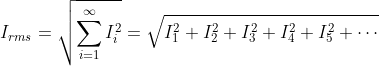
efektivna vrednost viši harmonici

Gornje formule su defnicija efektivne vrednosti napona, tj. struje u uslovima izobličenog signala. Instrumenti koji mere napon i struju prema ovoj formuli nazivaju se i TrueRMS ili TRMS instrumenti. Takvi instrumenti imaju kvalitetniji hardver, tj. mere i više harmonike. Instrumenti koji nemaju ovu funkciju „procenjuju“ efektivnu vrednost struje, najčešće slepo deleći amplitudu izmerenog signala sa $\sqrt{2}$ . Taj pristup daje korektan rezultat kada nema viših harmonika. Kada su prisutni viši harmonici neophodno je koristiti TRMS instrumente.

Zaključak: izobličenje struje je posledica rada nelinearnih uređaja u našim pogonima. Mi u praksi kažemo da je takva struja izobličena, i to implicira nešto loše, ali to samo znači da struja nije idealna sinusoida. Ništa više i ništa manje od toga. Važno je razumeti da je struja datog potrošača takva kakva je – složena, nije linearna u odnosu na napon. Radi se o fizičkoj karakteristici uređaja, načinu funkcionisanja, i u tome samo po sebi nema ništa loše.

THD faktor napona i struje

Mera odnosa viših harmonika i idealne sinusoide naziva se ukupno harmonijsko izobličenje ili THD (Total Harmonic Distortion). THD faktor se izražava u % i što je vrednost viša, izobličenje signala je veće. THD faktor se definiše kao odnos efektivne vrednosti svih prisutnih viših harmoničnih komponenti (i≥2) i efektivne vrednosti osnovnog harmonika (i=1).

$thd faktor viši harmonici$

Procentualno prisustvo viših harmonika u struji i naponu možemo najpre videti u povišenim vrednostima THD faktora, a potom analizom udela pojednačnih harmonika analizirati čije prisustvo je najuticajnije i najdominantnije.

Potrebno je obratiti pažnju da u režimima kada pogon ne radi, THD faktor struje može postići veoma visoke vrednosti, i preko 100%. Ovaj podatak često može da zbuni i uplaši. Međutim za to nema razloga, jer kada je struja pogona mala i struja osnovnog i struja viših harmonika su bliske nuli. Kada podelimo dve veličine bliske nuli dobijeni količnik može dobiti nerealno velike vrednosti.

Pogledajmo primere iz prakse:

Snaga i viši harmonici

Uspostavljanje i održanje tokova viših harmoničnih komponenti struja i napona nije besplatno. Nelinearni potrošači imaju velike prednosti po pitanju kontrolabilnosti, ali to ima svoju cenu. Osim energije na osnovnom harmoniku, koja će se konvertovati u koristan rad, sada postoje dodatne komponente snage na učestanostima viših harmonika.

Linearni potrošači

Kod linearnih potrošača, tj. onih koji ne generišu više harmonike, snaga se računa relativno jednostavno i to je ono što znamo iz škole. Odnos aktivne i reaktivne snage se formulom predstavlja kao S²=P²+Q². Ovaj odnos se može predstaviti i čuvenim vektorskim dijagramom, koji ste verovatno već viđali:

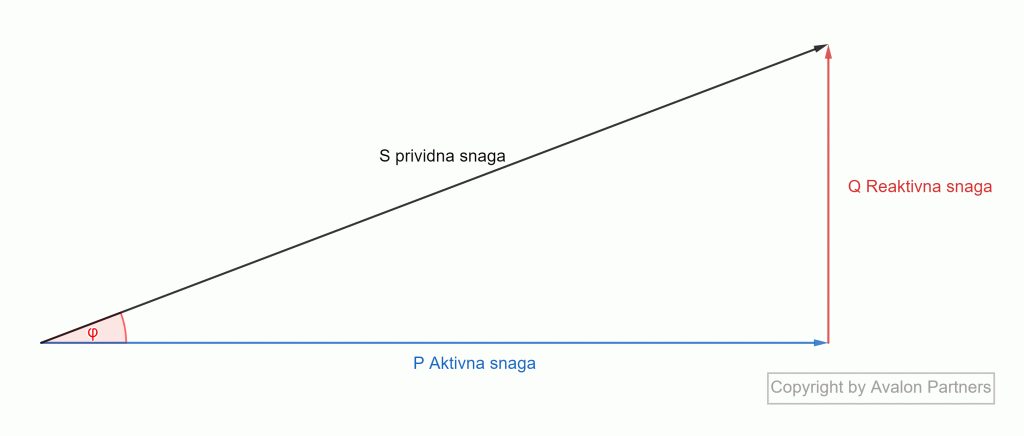
U sistemima gde je prisutan samo osnovni harmonik napona i struje, ugao $\varphi$ između prividne i aktivne snage je istovremeno i ugao koji odgovara faznom pomeraju: $\varphi =\measuredangle \left ( U,I \right )$ . Iz trougla snage sada je: $cos\left ( \varphi \right )=\frac{P}{S}$ . Aktivna snaga je: $P=U\cdot I\cdot cos\left ( \varphi \right )=S\cdot cos\left ( \varphi \right )$ . Odavde je faktor snage (odnos P i S) jednak . No, ovo je ono što znamo još iz Osnova elektrotehnike. Gornji dijagram može se pogledati i u interaktivnom obliku.

Ono što nije pokriveno Osnovama elektrotehnike je snaga nelinearnih potrošača.

Nelinearni potrošači

Rad nelinearnih potrošača pogoršava ukupni faktor snage sistema, jer se od ukupne energije predate potrošaču deo troši na aktivnu i reaktivnu energiju na osnovnom harmoniku, kao i kod linearnog potrošača, ali postoji i deo energije koji se troši samo na održanje tokova viših harmonika. U ovom trenutku postoji veći broj definicija reaktivne snage u prisustvu viših harmonika. Ovde ćemo predstaviti do nedavno važeću definiciju, zbog njene jednostavnosti i mogućnosti da se predstavi vektorskim dijagramom. Definicija reaktivne snage je sada unapređena i više o tome u posebnom članku.

Snaga distorzije

U prisustvu viših harmonika javlja se nova komponenta snage: Q_d – snaga distorzije, koja je direktna posledica interakcije napona i struja “zaprljanih“ višim harmonicima. Kako je aktivna snaga po definiciji vezana samo za osnovni harmonik, snaga distorzije ima karakter reaktivne snage jer sadrži samo komponente koje nisu na osnovnoj učestanosti. Odavde je već jasno da se Qd ne može pretvoriti u koristan rad i zbog toga sa porastom snage distorzije povećavaju se i gubici sistema.

Da bi pojednostavili objašnjenje, pretpostavićemo da je napon idealan, tj. da ima samo osnovni harmonik. Struja potrošača sadrži i osnovni i više harmonike. Prividna snaga ovakvog potrošača je:

S² = P² + Q1² + Qd²

P– aktivna snaga potrošača na osnovnom harmoniku.

Q1 – reaktivna snaga potrošača na osnovnom harmoniku

S1 – prividna snaga na osnovnom harmoniku $S_{1}=P^2+Q_{1}^2$

Qd – snaga distorzije potrošača, snaga viših harmonika kao posledica interakcije viših harmonika struje i osnovnog harmonika napona

Qtot – ukupna reaktivna snaga potrošača $Q_{tot}^2=Q_{1}^2+Q_{d}^2$

S – ukupna prividna snaga potrošača $S^2=P^2+Q_{tot}^2$

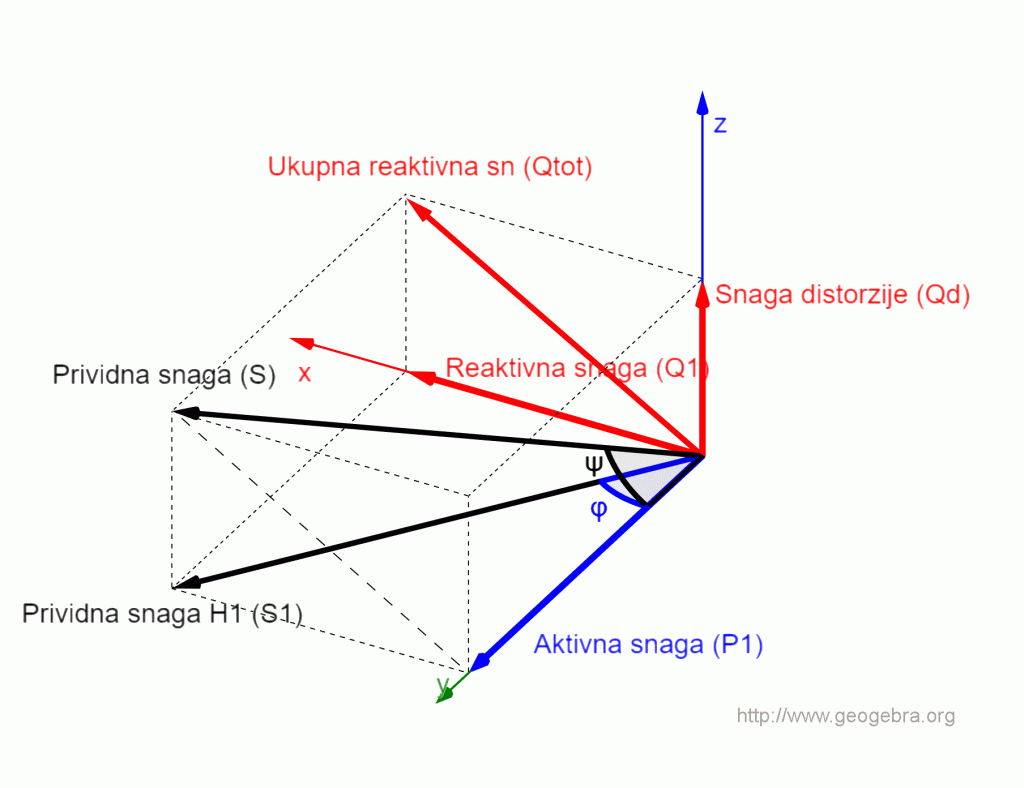
viši harmonici

Sa dijagrama je jasno da je, za istu aktivnu snagu, S veće od S1, tj. prividna snaga nelinearnog potrošača je veća od prividne snage linearnog potrošača. Time je faktor snage nelinearnog potrošača lošiji od faktora snage linearnog, za istu aktivnu snagu.

Evo kako prisustvo harmonika utiče na razliku između faktora snage i . Ugao $\varphi$ između osnovnog harmonika napona i osnovnog harmonika struje ostaje nepromenjen. Zbog toga što napon i struja sadrže pored osnovnog harmonika i više harmonične komponente, prividna snaga S je veća od prividne snage za osnovni harmonik S1. Sada je ugao između aktivne snage P i prividne snage S postao veći – na slici je označen sa $\psi$ . Faktor snage nelinearnog potrošača je $cos\left ( \psi \right )$ . Prikazani grafikon je interaktivan i možete se igrati sa snagama na sledećem linku.

Zbog ovoga uvodimo novi pojam: distorzioni faktor snage koji je mera za koliko se razlikuje od faktora snage, tj. od $cos\left ( \psi \right )$ .

DPF – distortion power factor

Ako zanemarimo sadržaj viših harmonika u naponu (tj. postoji samo osnovni harmonik napona) onda je:

$DPF=\frac{S_{1}}{S}=\frac{I_{1}}{\sqrt{I_{1}^2+I_{2}^2+I_{3}^2+I_{4}^2+I_{5}^2+\cdots}}$ . gde je DPF mera sadržaja viših harmonika.

$DPF=\frac{1}{\sqrt{1+\frac{I_{2}^2+I_{3}^2+I_{4}^2+I_{5}^2}{I_{1}^2}}}=\frac{1}{\sqrt{1+THD_{i}^2}}$

Sada se može definisati ukupni faktor snage:

$PF=\frac{P_1}{S}=\frac{S1\cdot cos\left ( \varphi \right )}{S}=cos\left ( \varphi \right )\cdot DPF=\frac{cos\left ( \varphi \right )}{\sqrt{1+THD_i^2}}$

Znači, u uslovima povišenog sadržaja viših harmonika, faktor snage tj. kosinus ugla između vektora P1 i S više nije jednak već je manji, srazmerno faktoru DPF. Ako to pogledamo sa strane potrošača, za istu aktivnu snagu koja se predaje potrošaču, u uslovima povišenog sadržaja viših harmonika, povećava se prividna snaga koju preuzimamo iz mreže. To povećanje troši se na održanje tokova viših harmonika a ne na koristan rad.

Važna posledica povećane vrednosti DPF-a je da kompenzacija reaktivne snage ne može minimizovati gubitke u pogonu. Potrebno je smanjiti i Qd, tj. THD struje i napona, da bi se prividna snaga pogona svela na minimum. Ovaj zadatak se može izvršiti tek stručnim merenjima i pažljivom analizom.

Viši harmonici i DPF sa stajališta elektroprivrede

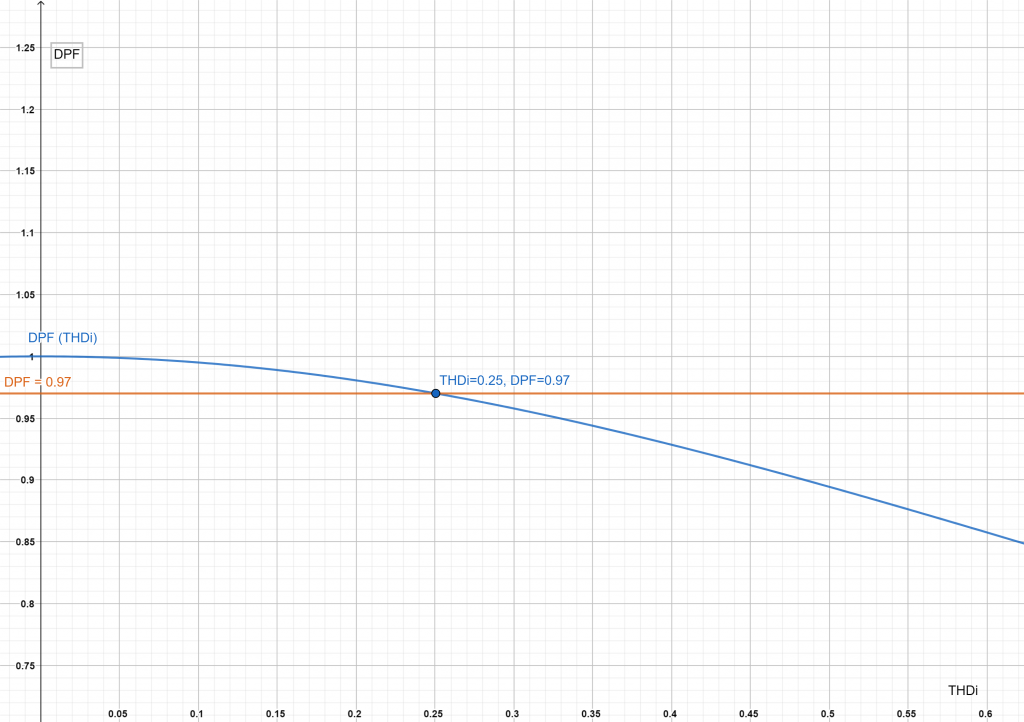
Na donjem grafikonu prikazana je zavisnost DPF od izobličenja struje. Za uobičajeni nivo izobličenja za industrijske potrošače od 25%, DPF iznosi 0,97. To znači da je realni faktor snage 3% manji od . I to u idealnom slučaju kada nema viših harmonika napona. Zašto je ovo bitno?

Tarifni sistem elektroprivrede predviđa da se obračun utrošene energije vrši na osnovnom harmoniku, tj. za faktor snage se usvaja . Tako obračunata energija se naplaćuje kupcima. Istovremeno ti isti kupci su prilično nelinearni potrošači. U rezidencijalnim sredinama dominantni potrošači su nelinearni: LED sijalice, napajanja računara, televizora,… punjači za telefone, ulično osvetljenje, itd. Klasični linearni potrošači poput TA peći, bojlera, ringle ili pećnice su u opadanju. U industrijskim sredinama sve je više nelinearnih potrošača: frekventni regulatori, servo pogoni, data centri, indukcione peći, ..

Veza između viših harmonika i gubitaka

U gore pomenutom primeru, prividna snaga je 3% veća nego što to brojilo električne energije pokazuje. Dodajte na to uticaj izobličenog napona, koji smo zbog jednostavnosti ovde izostavili, i dobićete mnogo veću grešku. Mi u praksi viđamo razlike između i DPF i do 15%-20%. Sada zaigrajmo igru velikih brojki i pomnožimo to sa brojem brojila u konzumu i otprilike dobijate sliku problema. Zbog ovoga mnoge elektroprivrede u svetu su prešle na obračun po faktoru snage a napustile su zastareli način obračuna po .

Smanjenje ovih gubitaka je interesantna tema i možete je usavršiti ako se prijavite na naše inhouse treninge iz kvaliteta napona. Tema za razmišljanje: ko plaća te povišene gubitke? Kada se fabrika koja ima visok udeo struja viših harmonika priključi na mrežu, koju komponentu reaktivne energije registruje merna grupa? Ko je tu na gubitku? Dodatna tema za razmišljanje, pre nego što se prijavite na naš inhouse trening, ako je napon u distributivnoj mreži izobličen (realno je THD u = oko 3%), da li linearni potrošači u vašoj fabrici imaju povećane gubitke? Ko je u toj situaciji na gubitku?